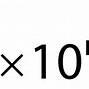
Rumus Perkalian di Microsoft Excel yang Paling Mudah
Plat nomor boleh ada angka yang sama, artinya angka yang sudah dipakai boleh dipakai lagi.
Kita buat 4 kota karena plat nomor terdiri dari 4 angka saja. Pilihan angkarnya adalah 1, 2, 3, 4, 5, artinya totalnya ada 5 pilihan angka. Cara pengisian setiap kotak:
- Kotak I, dapat diisi angka 1, 2, 3, 4, atau 5 sehingga ada 5 cara.
- Kotak II, dapat diisi dengan 5 pilihan angka juga karena angka yang sudah dipakai pada kotak I bisa dipakai lagi pada kotak II.
- Begitu juga dengan kotak III dan kotak IV ada 5 pilihan angka masing-masing. Banyaknya plat nomor = 5 × 5 × 5 × 5 = 625.
Jadi, banyaknya plat nomor yang bisa dibuat adalah 625 plat nomor.
3. Rahma mempunyai 6 buah kaus, 5 buah kemeja dan 4 buah celana panjang. Tentukan banyaknya variasi pakaian yang dapat dipakai Rahma?
Rahma dapat memakai kaus, kemeja, dan celana panjang secara bersamaan.
Jadi, dengan aturan perkalian banyak variasi pakaian yang dapat dipakai Rahma andra adalah:
Kaidah Pencacahan (Aturan Penjumlahan dan Aturan Perkalian
4. Suatu menu makan siang terdiri dari sayur, lauk, buah dan minuman masing-masing satu macam. Jika terdapat 3 macam sayur, 4 macam lauk, 5 macam buah dan 3 macam minuman. Berapakah banyaknya menu makan siang yang dapat dipilih?
Dengan aturan perkalian banyak menu yang dapat dipilih adalah:
Aturan Perkalian (Filling Slot)
5. Lea memiliki 3 baju yang berwarna Merah (M), Kuning (K) dan Putih (P). Selain itu ia juga memiliki celana yang berwarna Hitam (H) dan Coklat (C). Berapakah cara pemilihan pemasangan baju dan celana yang dapat digunakan oleh Lea?
Banyaknya cara pemilihan baju adalah 3 cara yaitu M, K dan P, sedangkan banyaknya cara pemilihan celana adalah 2 cara yaitu H dan C. Dengan demikian telah diketahui bahwa n1 = 3 dan n2 = 2.
Banyak cara pemilihan pasangan baju dan celana adalah 3 × 2 = 6.
Sedangkan pasangan baju dan celana tersebut adalah (1) MH, MC, (2) KH, KC, dan (3) PH, PC.
Itulah beberapa contoh soal aturan perkalian. Selamat mengerjakan.
Editor: Komaruddin Bagja
Pengertian Angka Penting
Angka penting merupakan semua angka yang didapatkan dari hasil pengukuran. Angka penting meliputi angka eksak dan satu angka terakhir yang ditaksir.
Baca berita dengan sedikit iklan, klik di sini
Angka bisa didapatkan dari hasil mengukur dan membilang. Adapun angka yang diperoleh dari hasil pengukuran disebut sebagai angka penting atau angka berarti, misalnya untuk menentukan luas tanah perkebunan. Sementara angka yang didapatkan dari hasil membilang dikenal sebagai angka eksak atau angka pasti, misalnya untuk mengetahui jumlah pohon yang ditanam.
Kemudian, menurut fisika.fmipa.unesa.ac.id, angka penting adalah angka hasil perhitungan yang didapatkan dari kegiatan pengukuran. Jumlah angka penting menunjukkan seberapa akurat dan seberapa teliti hasil pengukuran terhadap suatu besaran tertentu.
Berikut aturan penentuan jumlah digit pada hasil pengukuran angka penting:
- Semua angka bukan nol adalah angka penting. Misalnya, 2, 3, 4,5 mempunyai empat angka penting.
- Angka nol yang digunakan untuk tempat desimal bukanlah angka penting. Misalnya, 0,000012 mempunyai dua angka penting, yaitu 1 dan 2. Sementara empat angka 0 yang berada di sebelah kiri angka 12 dan di sebelah kanan koma tidaklah penting, karena angka taksiran seharusnya berada pada digit bagian akhir.
- Angka nol di belakang angka bukan nol dalam desimal adalah angka penting. Misalnya, 2,0 mempunyai dua angka penting, lalu 2,0400 mempunyai lima angka penting.
- Angka nol di sebelah angka bukan nol, tetapi tanpa tanda desimal, bukanlah angka penting, kecuali terdapat tanda khusus, seperti garis bawah. Misalnya 45000 mempunyai dua angka penting, sedangkan 45000 mempunyai tiga angka penting.
- Angka nol yang terletak di antara angka bukan nol merupakan angka penting. Misalnya 230,5 mempunyai empat angka penting.
Contoh Soal Penjumlahan
Ahmed memiliki beragam jenis kendaraan dengan jumlah yang berbeda-beda. Ia memiliki 4 buah mobil, 5 buah sepeda motor, dan 3 buah sepeda.
Dari keterangan tersebut, tentukan berapa jumlah cara Ahmed pergi ke kantor!
Perlu dipahami bahwa Ahmed hanya bisa mengendarai satu dari semua kendaraan yang Ia miliki. Mustahil baginya untuk mengendarai beberapa secara bersamaan.
Berdasarkan aturan penjumlahan, total jumlah cara yang bisa dilakukan Ahmed untuk pergi ke kantor ialah:
Jadi, Ahmed bisa ke kantor dengan menggunakan 12 cara.
Ella suka sekali mendengarkan musik dan dia ingin memperluas genre musik yang didengarkannya. Ia pun membuat sebuah daftar putar pada aplikasi streaming musik.
Daftar putar tersebut terdiri dari 5 lagu genre pop, 7 lagu genre jazz, dan 8 lagu genre opera. Dari data tersebut, tentukanlah ada berapa cara Ella bisa memilih lagu yang ingin Ia dengar!
Ella hanya bisa mendengarkan lagu pilihannya satu. Ia tidak bisa mendengarkannya secara bersamaan.
Berdasarkan aturan penjumlahan, maka total banyak cara Ella memilih lagu yang akan dinikmatinya adalah:
Jadi, ada 20 cara Ella bisa memilih lagu untuk didengarkan.
Itulah bagian pertama dari contoh soal aturan penjumlahan, perkalian, permutasi, dan kombinasi. Yuk, lanjut pelajari bagian contoh soal aturan perkalian di bawah!
Beberapa Contoh Soal Aturan Penjumlahan, Perkalian, Permutasi, dan Kombinasi
Contoh Soal Aturan Perkalian beserta Jawabannya SMA Kelas 12
Berikut ini beberapa contoh soal aturan penjumlahan, perkalian, permutasi, dan kombinasi lengkap dengan pembahasannya:
Contoh Soal Permutasi
Sebuah kaleng bekas biskuit dijadikan tempat beberapa warna benang jahit.
Jumlahnya ada 7 benang jahit dengan warna yang berbeda-beda. 3 benang berwarna hitam, 2 benang berwarna merah, dan 2 benang berwarna putih.
Bila gulungan benang tersebut secara teratur disusun sebaris, tentukanlah berapa banyak variasi susunan yang bisa tercipta!
P = 7 x 6 x 5 x 4 x 3 x 2 x 1 / ( 3 x 2 x 1 ) ( 2 x 1 ) ( 2 x 1 )
P = 7 x 6 x 5 x 4 / 4
Jadi, variasi susunan yang bisa tercipta dari 7 benang berbeda warna adalah 210 variasi.
Sebuah organisasi baru saja terbentuk dan ingin membuat susunan kepengurusan.
Diketahui jumlah anggota saat ini ada sebanyak 10 anggota. Posisi yang dibutuhkan adalah ketua, wakil, bendahara, sekretaris, dan pengawas.
Dari data tersebut, tentukanlah berapa peluang variasi dari susunan panitia yang bisa tercipta!
10P5 = 10! / ( 10 – 5 )!
10P5 = (10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1) / (5 x 4 x 3 x 2 x 1)
10P5 = 10 x 9 x 8 x 7 x 6
Jadi, jumlah variasi dari susunan pengurus yang bisa tercipta adalah 30240.
Sebuah presentasi akan dilakukan dan masing-masing kelompok berjumlah 4 orang. Tentukan berapa variasi dari tempat duduk yang bisa dibuat!
Jadi, jumlah variasi tempat duduk yang bisa tercipta adalah 6.
Itulah bagian ketiga dari contoh soal aturan penjumlahan, perkalian, permutasi, dan kombinasi. Yuk, lanjut pelajari bagian contoh soal kombinasi di bawah!
Contoh Soal Penalaran Matematika Persiapan SNBT 2023 Beserta Jawabannya
Pengaturan angka penting
Dilansir dari Khan Academy, angka penting adalah jumlah suatu nilai hasil pengukuran yang berkontribusi pada tingkat keakuratan nilai.
Sederhananya, angka penting adalah angka yang didapat dari hasil suatu pengukuran.
Baca juga: Pengukuran: Pengertian Para Ahli, Macam, Cara Penggunaan, dan Rumusnya
Angka penting terdiri dari angka pasti dan angka taksiran. Angka pasti adalah angka yang diperoleh dari skala alat ukur.
Sedangkan, angka taksiran adalah angka yang diperoleh dari satuan skala terkecil atau angka ketelitian alat ukur.
Penentuan angka penting memiliki aturan tertentu. Aturan angka penting adalah:
Baca juga: Bilangan yang Terdiri atas Tiga Angka yang Jumlahnya 9
Untuk lebih memahami tentang aturan angka penting, berikut adalah penjelasan dan contoh dari aturan angka penting!
Perkalian dan Pembagian
Penulisan jumlah angka penting hasil perkalian atau pembagian sama dengan jumlah angka penting paling sedikit dari bilangan-bilangan yang dioperasikan. Misalnya, hasil perkalian antara 1,6283 cm (4 angka penting) dengan 2,2 cm (2 angka penting) adalah 1,8226 cm. Maka, hasil akhirnya harus dituliskan menjadi 1,8 cm (2 angka penting).
Sementara itu, perkalian angka antara hasil pengukuran dengan hasil membilang, hasil akhirnya harus mempunyai jumlah angka penting paling sedikit yang sama dengan angka penting pada hasil pengukuran.
Misalnya, keramik lantai mempunyai panjang 50,25 cm dan lebar 20,1 cm (panjang dan lebar adalah angka dari hasil pengukuran). Apabila terdapat 25 buah keramik (jumlah angka dari hasil membilang) yang digunakan untuk menutup lantai, maka berapakah luas lantai yang tertutup keramik?
- Panjang = 50,25 cm (4 angka penting), lebar = 20,1 cm (3 angka penting), dan jumlah keramik = 25 keramik (dua angka penting).
- Untuk mengukur luas lantai = panjang x lebar x jumlah keramik = 50,25 x 20,1 x 25 = 25.250,625 cm2.
- Maka, hasil akhirnya harus ditulis 25.200 atau 2,52 x 104 cm2 (3 angka penting).
Dalam menuliskan angka penting tersebut berlaku aturan pembulatan angka 5. Jika sebelum angka 5 terdapat bilangan ganjil, maka dibulatkan ke atas. Sementara apabila sebelum angka 5 terdapat bilangan genap, maka angka 5 dihilangkan. Misalnya, 2,25 menjadi 2,2 dan 2,35 menjadi 2,4.
Jumlah angka penting dari hasil perhitungan pangkat atau akar harus mempunyai jumlah angka penting yang sama dengan yang dioperasikan. Misalnya:
- Akar dari 2,25 adalah 1,5, lalu ditulis menjadi 1,50.
- Pangkat dua dari 2,5 adalah 6,25, lalu ditulis menjadi 6,2 (berlaku aturan pembulatan angka 5).
KOMPAS.com – Dalam suatu bilangan, tidak semua angka merupakan angka penting. Apa yang dimaksud dengan angka penting? Berikut adalah pengertian, aturan, dan contohnya!
Angka penting atau significant figures menjadi salah satu konsep perhitungan yang diajarkan guru kepada peserta didik di satuan pendidikan. Materi terkait angka penting umumnya diperkenalkan sejak duduk di bangku kelas X sekolah menengah atas (SMA) melalui mata pelajaran Fisika.
Melansir Modul Pembelajaran SMA Kelas X karya Saroji (2020), angka penting terdiri dari angka pasti dan angka taksiran atau angka yang diragukan. Lantas, apa itu angka penting?
Tabel Perkalian 1-10 dan Cara agar Cepat Menghafal Perkalian
2. Rendy ingin membuatkan plat nomor kendaraan yang terdiri dari 4 angka yang dipilih dari angka-angka 1, 2, 3, 4, 5 dan dalam plat nomor itu boleh ada angka yang sama. Berapa banyak plat nomor dapat dibuat?
Penjumlahan dan Pengurangan
Angka hasil penjumlahan atau pengurangan hanya boleh dituliskan satu angka taksiran. Misalnya, hasil penjumlahan 3,219 cm; 15,5 cm; dan 8,43 cm adalah 27,149 cm. Maka, hasil akhirnya harus dituliskan menjadi 27,1 cm, sehingga hanya memiliki satu angka taksiran.